Deepfm模型解析
Deepfm模型解析
简介
对于一个基于CTR预估的推荐系统,最重要的是学习到用户点击行为背后隐含的特征组合。在不同的推荐场景中,低阶组合特征或者高阶组合特征可能都会对最终的CTR产生影响。但是现存的方法总是忽视了高阶或低阶组合特征的联系,或者要求专门的特征工程,因此建立了DeepFM模型,将FM与DNN结合起来。
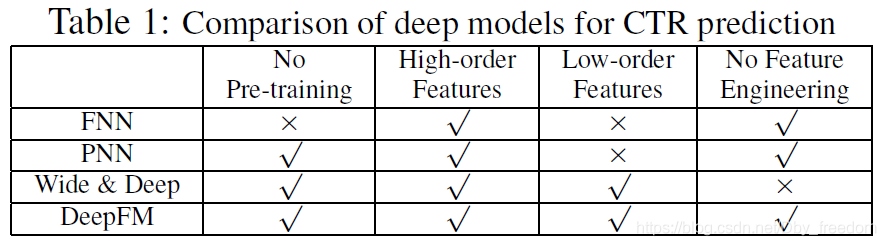
模型演变和各模型间的对比
CTR的任务要求
CTR的数据特点
1、输入中包含类别型和连续型数据。类别型数据需要one-hot,连续型数据可以先离散化再one-hot,也可以直接保留原值
2、维度非常高且数据非常稀疏
CTR的预估重点
CTR预估重点在于学习组合特征。
其中,组合特征包括二阶、三阶甚至更高阶的,阶数越高越复杂,越不容易学习。Google的论文研究得出结论:高阶和低阶的组合特征都非常重要,同时学习到这两种组合特征的性能要比只考虑其中一种的性能要好。
那么关键问题转化成:如何高效的提取这些组合特征。
一种办法就是引入领域知识人工进行特征工程。这样做的弊端是高阶组合特征非常难提取,会耗费极大的人力。而且,有些组合特征是隐藏在数据中的,即使是专家也不一定能提取出来,比如著名的“尿布与啤酒”问题。
DeepFM模型的引入
为了解决上文提到的提取组合特征的问题,该论文作者借鉴了Google的wide & deep的做法提出了DeepFM模型。
DeepFM模型本质是
1、将Wide & Deep 部分的wide部分由 人工特征工程+LR 转换为FM模型,避开了人工特征工程;
2、FM模型与deep part共享feature embedding。
Q1、为什么要用FM代替线性部分(wide)呢?
因为线性模型有个致命的缺点:无法提取高阶的组合特征。
FM通过隐向量latent vector做内积来表示组合特征,从理论上解决了低阶和高阶组合特征提取的问题。但是实际应用中受限于计算复杂度,一般也就只考虑到2阶交叉特征。
各模型间的对比
1、随着DNN在图像、语音、NLP等领域取得突破,人们意识到DNN在特征表示上的天然优势。相继提出了使用CNN或RNN来做CTR预估的模型。但是,CNN模型的缺点是:偏向于学习相邻特征的组合特征。RNN模型的缺点是:比较适用于有序列(时序)关系的数据。
2、FNN (Factorization-machine supported Neural Network) 的提出,应该算是一次非常不错的尝试:先使用预先训练好的FM,得到隐向量,然后作为DNN的输入来训练模型。缺点在于:受限于FM预训练的效果。
3、PNN (Product-based Neural Network),PNN为了捕获高阶组合特征,在embedding layer和first hidden layer之间增加了一个product layer。根据product layer使用内积、外积、混合分别衍生出IPNN, OPNN, PNN*三种类型。无论是FNN还是PNN,他们都有一个绕不过去的缺点:对于低阶的组合特征,学习到的比较少。而前面我们说过,低阶特征对于CTR也是非常重要的。
4、为了同时学习低阶和高阶组合特征,Google提出了Wide&Deep模型。它混合了一个线性模型(Wide part)和Deep模型(Deep part)。这两部分模型需要不同的输入,而Wide part部分的输入,依旧依赖人工特征工程。
DeepFM优势
3中的这些模型普遍都存在两个问题:
偏向于提取低阶或者高阶的组合特征。不能同时提取这两种类型的特征。
需要专业的领域知识来做特征工程。
DeepFM在Wide&Deep的基础上进行改进,成功解决了这两个问题,并做了一些改进,其优势如下:
1.不需要预训练FM得到隐向量
2.不需要人工特征工程
3.能同时学习低阶和高阶的组合特征
4.FM模块和Deep模块共享Feature Embedding部分,可以更快的训练,以及更精确的训练学习
Deepfm模型介绍
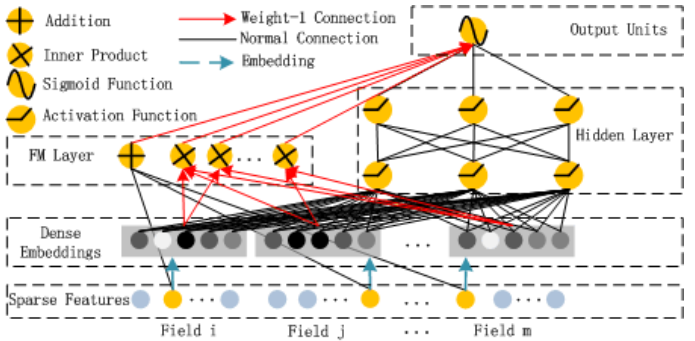
Sparse Feature部分
Sparse Feature是指离散型变量。比如现在我有数据:xx公司每个员工的姓名、年龄、岗位、收入的表格,那么年龄和岗位就属于离散型变量,而收入则称为连续型变量。这从字面意思也能够理解。
现在Sparse Feature里表示的是将每个特征经过one-hot编码后拼接在一起的稀疏长向量,黄色的点表示某对象在该特征的取值中属于该位置的值。
Dense Embedding部分
Embeddings in Machine Learning: Everything You Need to Know | FeatureForm
原理
这个长长的向量只有0,1两种取值,并且非常稀疏,如果直接采用权重去加和,将会丢失很多权重,这样会造成最终结果不准确。所以,得想个办法把这个稀疏向量变得稠密一些。在机器学习中关于对离散值的数据预处理有很多种方式,常见的有数据分箱、嵌入向量等,这个Dense Embedding就是指的将离散型变量嵌入为连续型变量。什么意思呢?
还是上面说的那个表格,比如年龄共有50个去重数值,岗位有100个去重数值,现在是两个特征。那么经过Embedding之后,年龄就变为了50 x m的矩阵,岗位就变成了100 x m的矩阵,这个m是指嵌入向量的维数,一般取4、8、16。下面的图示可能会比较直观一些:

最终表格就变成了这样:
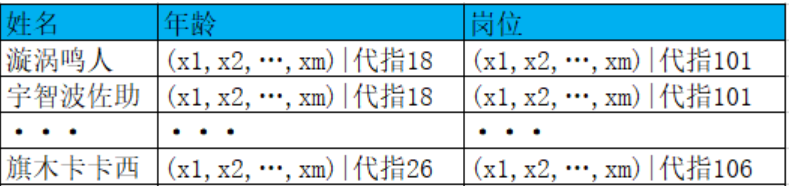
也就是说,最终入模的数据表长这样:

比如“漩涡鸣人”的特征向量可能就是这样的:
(x1,x2,…,xm,x1,x2,…,xm,…,···,x1,x2,…,xn)
x1,x2,…,xm 表示他的年龄的Embedding向量,x1,x2,…,xm 表示他的岗位的Embedding向量,… 表示他的其他属性的Embedding向量,x1,x2,…,xn 表示他的收入等其他连续型特征的归一化或标准化后的值。
一句话,就是拼接起来。
实现
1 | embedding = tf.constant( |
在embedding_lookup中,第一个参数相当于一个二维的词表,并根据第二个参数中指定的索引,去词表中寻找并返回对应的行。上面的过程为:

注意这里的维度的变化,假设我们的feature_batch 是 1维的tensor,长度为4,而embedding的长度为4,那么得到的结果是 4 * 4 的,同理,假设feature_batch是2 *4的,embedding_lookup后的结果是2 * 4 * 4。
embedding层其实是一个全连接神经网络层,那么其过程等价于:

可以得到下面的代码:
1 | embedding = tf.constant( |
二者是否一致呢?我们通过代码来验证一下:
1 | with tf.Session() as sess: |
二者得到的结果是一致的。
因此,使用embedding_lookup的话,我们不需要将数据转换为one-hot形式,只需要传入对应的feature的index即可。
FM Layer部分
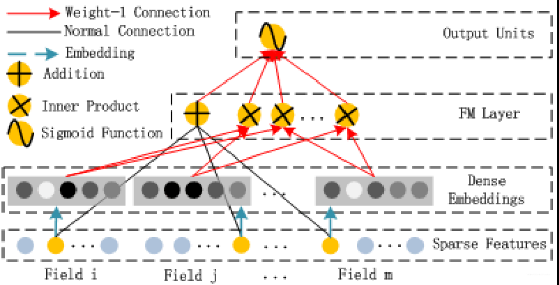
主要公式:
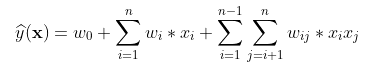
FM的公式,以及二次项的化简过程:
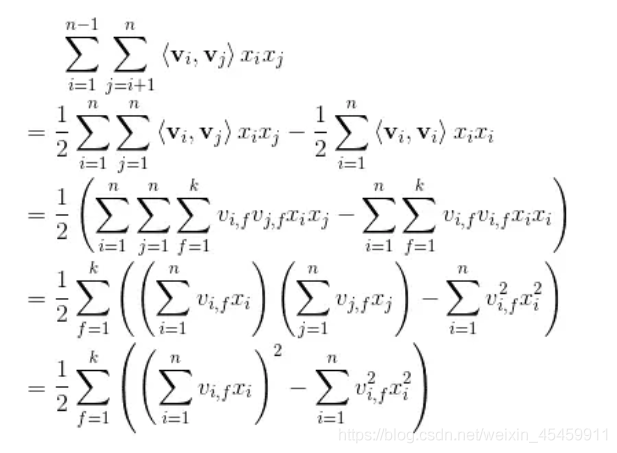
对于二次项,经过化简之后有两部分(暂不考虑最外层的求和),我们先用excel来形象展示一下两部分,这有助于你对下面代码的理解。
第一部分过程如下:
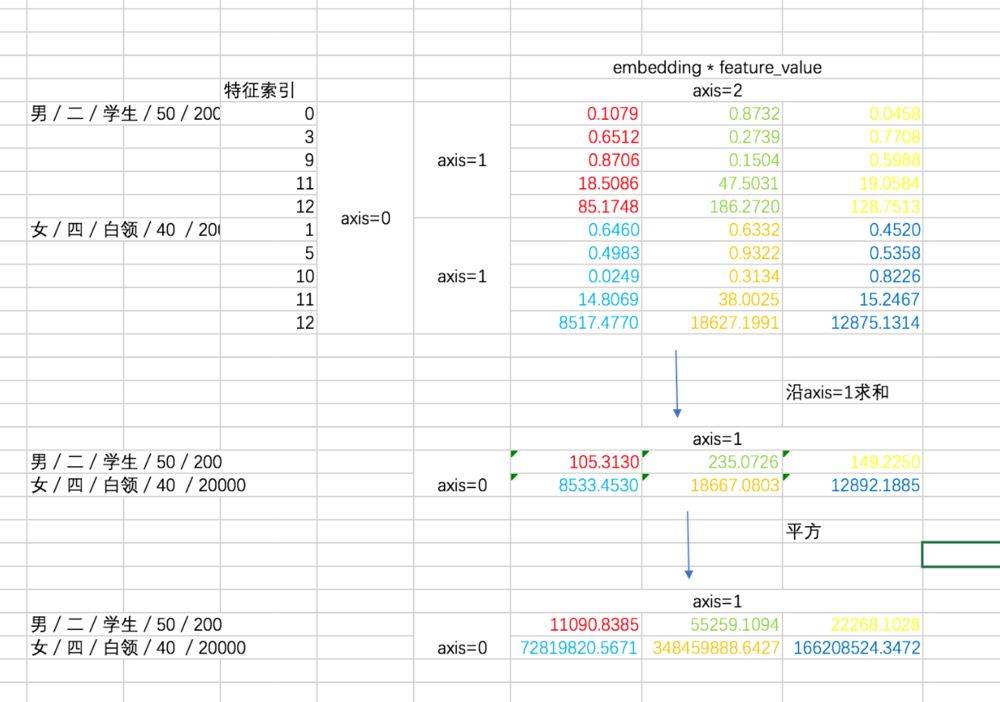
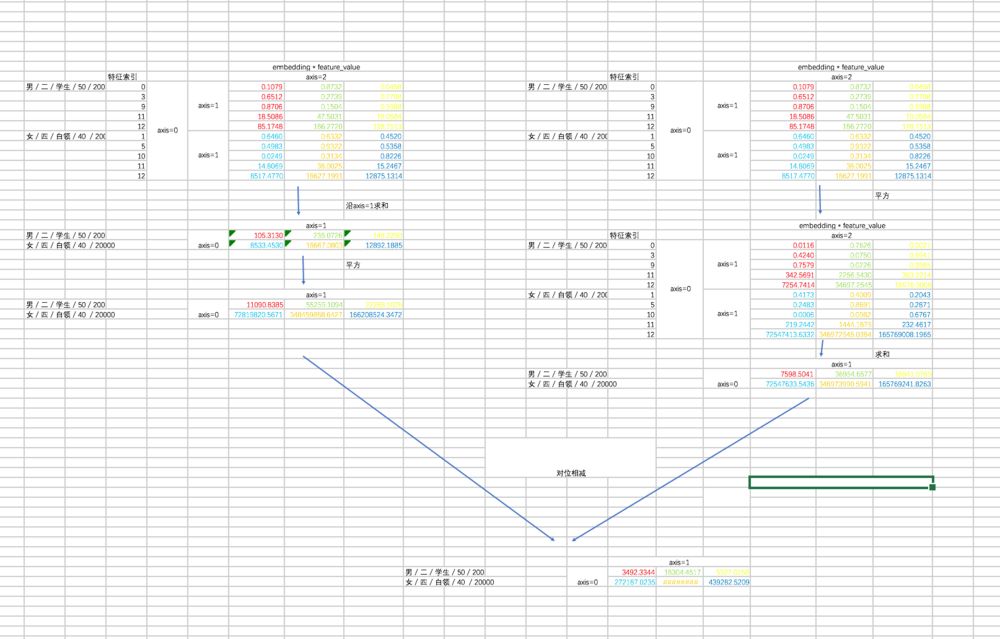
第二部分的过程如下:

最后两部分相减:
转换完变成以下公式:
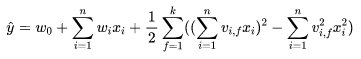
Hidden Layer部分
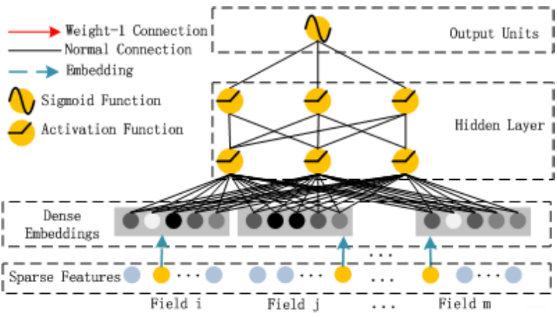
Deep Component是用来学习高阶组合特征的。网络里面黑色的线是全连接层,参数需要神经网络去学习。
Deep部分很简单了,就是几层全连接的神经网络:
1 | """deep part""" |
Outputs Units部分
对象的特征先经过one-hot编码变为稀疏长向量,再通过Embedding变为统一长度的稠密向量,然后在FM结构中显示交互作用,以及在DNN结构中隐式交互作用,最后水到渠成就该输出预测目标值了。即:
如果是分类任务,那么就将两者的值相加再输入Sigmoid函数输出类别概率大小。
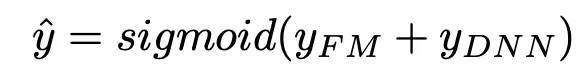
如果是回归任务,那么就直接将两者的值相加。
核心的计算过程
(1)首先进行样本embedding结果的获取,针对每个样本,会根据其具有的特征索引列表feat_index,获取这些特征对应在weights[‘feature_embeddings’] 矩阵中所存储的embeding表达形式。之后我们样本原值, 利用embeding表达形式【维度 是 field长度 * embeding长度】 * 样本原值【维度是field长度】 得到当前样本的 embedding转换结果 【维度是 field长度 * embeding长度】,这里样本的特征长度都是field长度,权重矩阵中的特征长度则是feature_size。
1 | self.embeddings =tf.nn.embedding_lookup(self.weights['feature_embeddings'],self.feat_index) # N * F * K |
(2)进行FM部分的计算,FM部分可以分为一阶计算 和 二阶计算两部分。首先是一阶计算阶段, 其直接使用W *x计算结果即可,没做embeding.
1 | self.y_first_order = tf.nn.embedding_lookup(self.weights['feature_bias'],self.feat_index) |
在二阶计算部分,对应如下的对FM转化的公式(优化后公式简单相当多),这里的u其实就是weights[‘feature_embeddings’]隐向量矩阵,u*x已经在第一部分做embedding时候做过了,剩余的就是 对两两内积结果的组内相加等操作
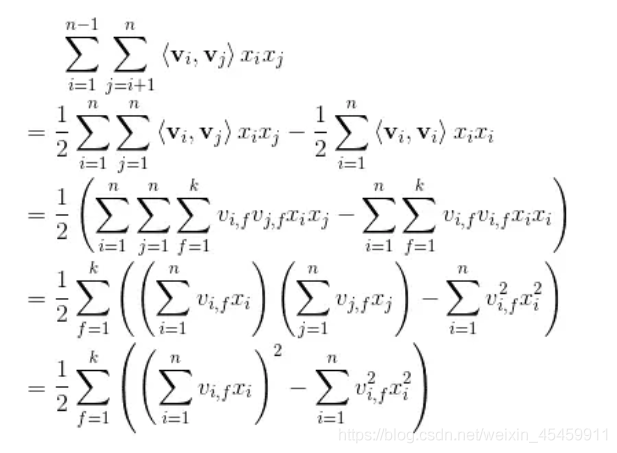
对应代码如下,每个样本都是对应下面的过程,两部分的相减。
1 | #second order term 这整体区间代表FM公式中的二次项计算 |
(3)最后是深度deep计算,这部分就是典型的DNN的方式,从embedidng结果开始【尺寸是field_size * embedding_size】,定义几层全连接计算即可。
1 | Deep component 将Embedding part的输出再经过几层全链接层 |
至此已经完成了核心的计算过程。
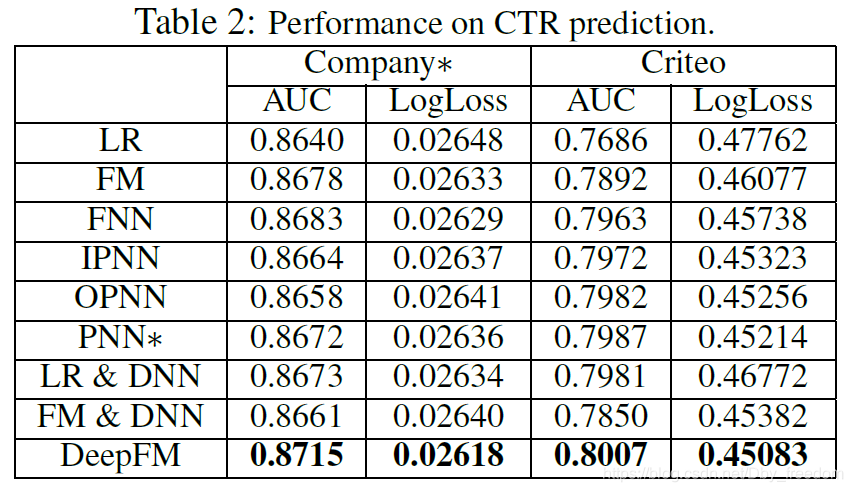
模型效果对比